Авторы: Ирматов Анвар, Белоуcов Алекcандр,КАДОУРИ Эйтан (US), Грачев Андрей, Рыжов Алекcандр, ТЕНИ Лоран (FR)
Изобретение отноcитcя к cредcтвам для выполнения экcтракции и раcпознавания многоугольников для cредcтв автоматизации электронного проектирования, применяемых при проектировании интегральных схем. Техническим результатом является уменьшение объема требуемых данных для обработки, а также улучшенный подход к перестройке топологических данных и созданию иерархии для лучшей и более эффективной обработки. Кластеры элементов экстрагируются и затем обрабатываются отдельно. При некоторых подходах множество многоугольников образует кластер, если для любых двух многоугольников из множества существует последовательность многоугольников таким образом, что расстояние между последовательными многоугольниками является меньшим или равным данному пороговому числу. Вместо анализа каждого отдельного многоугольника в модели повторяющиеся уникальные структуры анализируются однократно, а затем воспроизводятся для всех кластеров, имеющих одинаковую повторяющуюся структуру. 9 ил.
Уровень техники
ИС представляет собой небольшое электронное устройство, созданное из полупроводникового материала. Каждая ИС содержит большое количество электронных комплектующих, например транзисторов, собранных для образования автономного схемного устройства. Комплектующие и межсоединения на ИС образуются как серия геометрических форм или многоугольников, расположенных и трассированных на материале кристаллов микросхем. Во время установки, местонахождение и размещение каждой геометрической формы, соответствующее компоненту ИС, идентифицируется на слоях ИС. Во время трассирования серия разводок идентифицируется для связывания геометрических форм для электронных комплектующих.
После завершения топологии необходимо подтверждение ее соответствия правилам проектирования, что обычно производится литейным производством, изготавливающим устройство ИС. Этот процесс верификации называется "Проверка правил проектирования (DRC)". Правила проектирования представляют собой набор правил в отношении минимальных расстояний, размеров, критериев для корпусов, наряду с другими ограничениями осуществления топологии. Эти правила необходимо выполнять для обеспечения максимальных возможностей успешного изготовления интегральной схемы.
Многочисленные иные типы операций и анализов могут также производиться на серии многоугольников, образующих ИС. Например, многоугольники могут анализироваться для определения того, должна ли к ним применяться корректировка оптической близости (ОРС). ОРС относится к процессу добавления дополнительных многоугольников к шаблону для изготовления ИС с целью корректирования любых ожидаемых оптических эффектов, существование которых может вызвать ошибки или неточности в форме комплектующих конечной изготовленной интегральной схемы, являющихся результатом литографического процесса формирования интегральной схемы. Типичным примером операции ОРС является анализ проектирования ИС для определения наличия многоугольников с сегментом или стенкой, недостаточно близкой к другому многоугольнику, что может привести к искривленному сегменту в конечной интегральной схеме из-за оптических эффектов литографического процесса. Для исправления оптического эффекта такого типа рассеивающий стержень, ниже разрешающего предела литографического оборудования, добавляется параллельно рассматриваемому сегменту. Этот рассеивающий стержень приведет к тому, что литографическое оборудование изготовит более прямой сегмент или стенку для многоугольника.
Учитывая большое количество комплектующих в типичной ИС, нередко требуется значительное время и существенный объем ресурсов системы (и ЦПУ, и ЗУ) для выполнения серии операций или анализа данного типа ИС. В частности, рассмотрим тип ИС со многими миллионами многоугольников. Каждый многоугольник потенциально нуждается в проведении анализа и операций для определения, например, применимости рассеивающих стержней. В качестве другого примера можно указать, что каждый из миллионов многоугольников требует проверки для определения и идентификации любых отклонений от правил DRC.
В связи с резким ростом сложности и размера данных топологии для нового поколения интегральных схем (ИС) существующие методы организации данных по ИС становятся все более недостаточными для обеспечения эффективного доступа и анализа данных.
Сущность изобретения
Поэтому для решения вышеуказанных и других проблем на основе предшествующих подходов реализация настоящего изобретения обеспечивает лучший подход к организации, анализу и работе с данными о многоугольниках, что значительно уменьшает объем требуемых данных для обработки, одновременно не допуская взаимного сопряжения элементов.
В соответствии с одним методом экстрагируются кластеры элементов, которые затем обрабатываются по отдельности. При некоторых методах серия многоугольников образует кластер, если для любых двух многоугольников из серии кластеров существует последовательность многоугольников, где расстояние между последовательными многоугольниками меньше или равно данному пороговому числу. Вместо анализа каждого отдельного многоугольника схемы один раз анализируются повторяющиеся уникальные модели, которые затем повторяются для всех кластеров, обладающих одинаковой повторяющейся моделью. Дальнейшие детали аспектов, объектов и преимуществ настоящего изобретения даны ниже в подробном описании, чертежах и заявках. И вышеприведенное общее описание, и последующее подробное описание являются иллюстративными и пояснительными и они не представляют собой ограничения объема изобретения.
Краткое описание чертежей
На фиг.1 дается блок-схема процесса экстракции и распознавания типа интегральной схемы в соответствии с некоторыми вариантами исполнения изобретения.
На фиг.2А-Е дается иллюстративный пример экстракции и распознавания многоугольников в типе интегральной схемы, в соответствии с некоторыми вариантами исполнения изобретения.
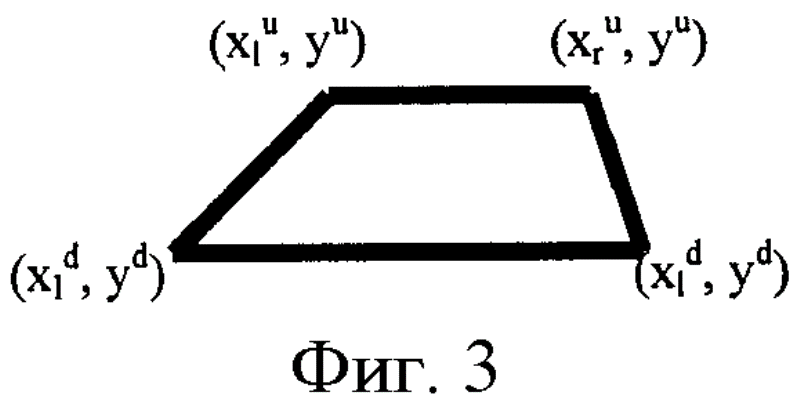
На фиг.3 показан пример трапеции, примененный в исполнении изобретения.
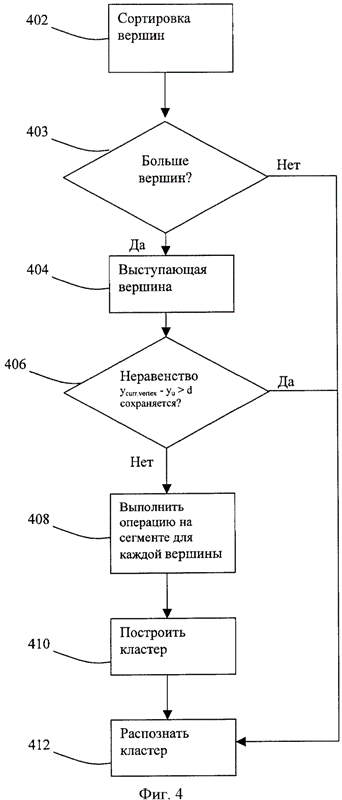
На фиг.4 приведена блок-схема процесса для кластеризации многоугольников в соответствии и некоторыми вариантами исполнения изобретения.
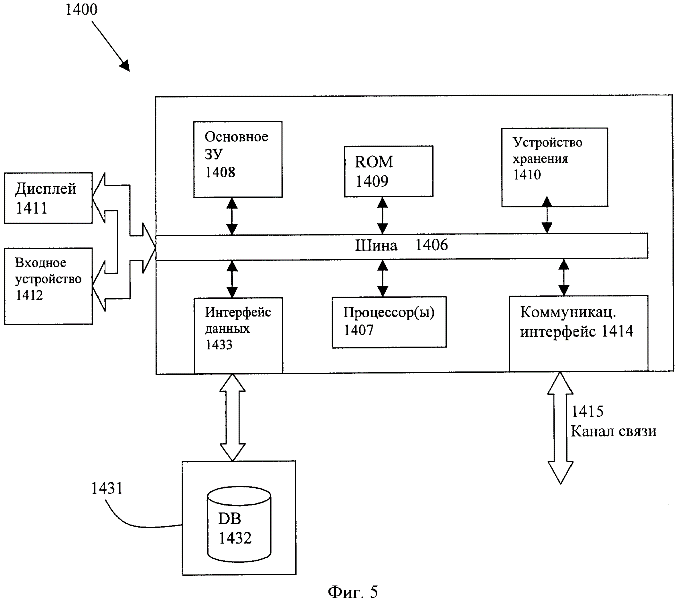
На фиг.5 дается пример архитектуры вычислительной системы, которая может применяться в исполнении изобретения.
Подробное описание изобретения
Исполнение настоящего изобретения предлагает улучшенный подход к организации, анализу и применению данных о многоугольниках, необходимых для обработки, одновременно не допуская взаимного сопряжения элементов. Исполнение изобретения дает улучшенный подход к перестройке топологических данных и созданию иерархии для лучшей и более эффективной обработки. Раскрывается автоматизированный метод формирования кластеров из многоугольников и метод кодирования серии многоугольников в данной топологии в форме древовидной структуры. Автоматизированный метод образования кластеров из многоугольников обеспечивает выбор подмножества форм, не воздействующих на другие формы, а также дает кодировку для множества в данной топологии в форме древовидной структуры, что позволяет распознавание повторяющихся типов топологических данных. Результат включает множества форм (
кластеры
), выбранных из топологии, которые неоднократно повторяются, но не влияют друг на друга при будущей обработке. Исходное множество форм может обрабатываться отдельно. С уменьшением общего количества форм из-за повторения структуры для дальнейшей обработки требуется меньше ресурсов по сравнению с первоначальными методами.
Подход, применяемый при некоторых исполнениях настоящего изобретения, захватывает весь объем данных за один раз и осуществляется в течение времени О(n log n), используя оперативную память O(n0,5). Он распознает все кластеры в данном слое и образует список классов эквивалентных кластеров, существующих в слое. Для любого данного кластера в слое он обнаруживает класс эквивалентности, в котором он содержится, из списка классов эквивалентных кластеров.
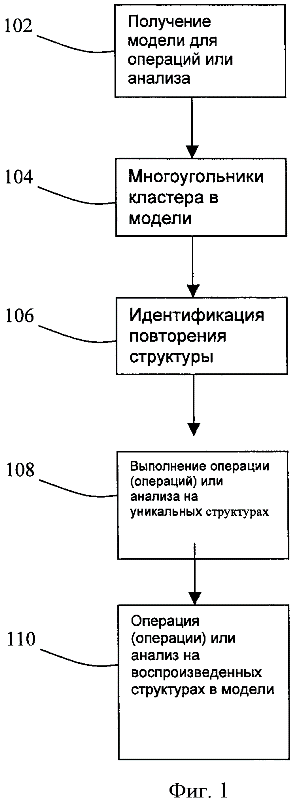
На фиг.1 показана блок-схема процесса экстракции и распознавания многоугольников в соответствии с исполнением изобретения. На этапе 102 процесс получает тип ИС для анализа и осуществления. Тип ИС включает физическую модель, осуществленную в виде множества геометрических форм или многоугольников.
На этапе 104 экстрагируются кластеры элементов, которые затем обрабатываются по отдельности. При некоторых способах исполнения множество многоугольников образует кластер, если для любых двух многоугольников из множества существует последовательность многоугольников из множества, когда расстояние между последовательными многоугольниками меньше или равно данному пороговому числу. Повторяющиеся структуры идентифицируются внутри различных кластеров (106). Вместо анализа каждого отдельного многоугольника в модели, повторяющиеся уникальные структуры анализируются один раз (108) и затем воспроизводятся для всех кластеров, имеющих такую же повторяющуюся структуру (110).
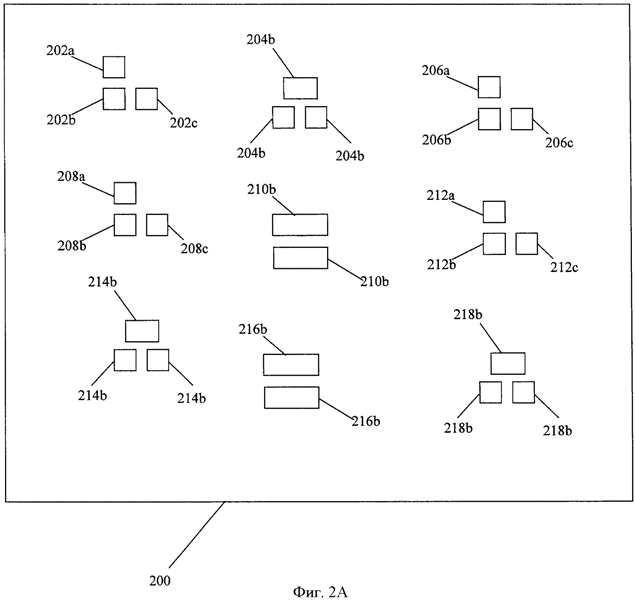
Для иллюстрации этого процесса следует рассмотреть в качестве образца множество многоугольников, показанное на фиг.2А. Это множество 200 многоугольников включает 31 различный многоугольник 202а-с, 204а-с, 20ба-с, 208а-с, 210a-b, 212a-c, 214a-c, 216a-b и 218а-с. Представим себе, что желательно выполнить какого-либо рода анализ автоматизации электронного проектирования (EDA) или операцию на этом множестве 200 из 31 многоугольника. Например, предположим, что желательно произвести ОРС (корректировку оптической близости) для определения необходимости и способа включения рассеивающих стержней в модель ИС. При обычной обработке, многоугольник во множестве 200 должен индивидуально рассматриваться и обрабатываться для идентификации рассеивающих стержней, которые необходимо включить в модель.
В этом примере, основанном на только 31 многоугольнике на фиг.2А, не требуется чрезмерных вычислительных ресурсов для выполнения такого типа анализа на каждом многоугольнике. Однако в типичных моделях ИС это число многократно умножается, поскольку вполне возможно существование крайне большого количества многоугольников в этой модели, например, много миллионов многоугольников. При наличии многих миллионов многоугольников и если каждый многоугольник необходимо обрабатывать отдельно, то, вероятно, потребуется действительно огромное количество времени и вычислительных ресурсов для осуществления требуемой обработки. Это является примером того типа проблем, с которыми сталкиваются многие средства EDA, поскольку может потребоваться рассмотрение каждого из этих миллионов многоугольников для выполнения требуемого анализа или операции с помощью обычных средств EDA.
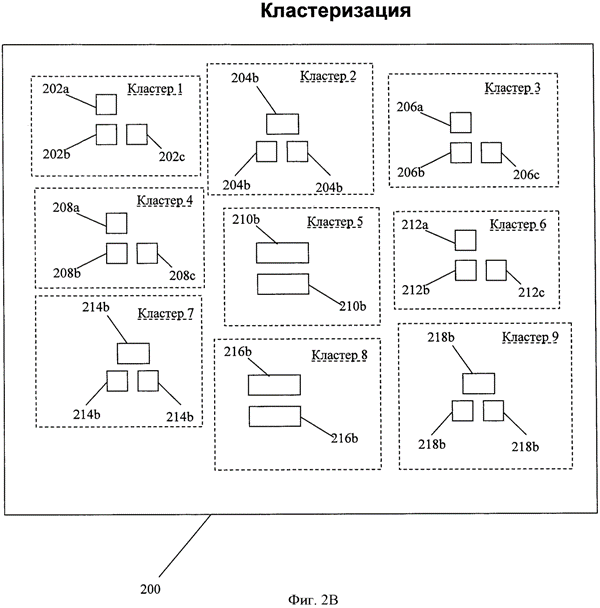
Вместо этого исполнение настоящего изобретения будет включать кластеризацию для того, чтобы избежать многих проблем, отмеченных у прототипа. Как отмечалось выше, множество многоугольников образует кластер, если для любых двух многоугольников из множества существует последовательность многоугольников из множества таким образом, что расстояние между любыми последовательными многоугольниками меньше или равно данному пороговому числу. Например, множество 200 многоугольников показано на фиг.2A, множество из девяти кластеров может быть образовано так, как показано на фиг.2В. В частности, многоугольники 202а, 202b и 202с собираются как кластер 1. Аналогичным образом многоугольники 204а-с образуют кластер 2, многоугольники 206а-с образуют кластер 3, многоугольники 208а-с образуют кластер 4, многоугольники 210а-b образуют кластер 5, многоугольники 212а-с образуют кластер 6, многоугольники 214а-с образуют кластер 7, многоугольники 216а-b образуют кластер 8 и многоугольники 218а-с образуют кластер 9.
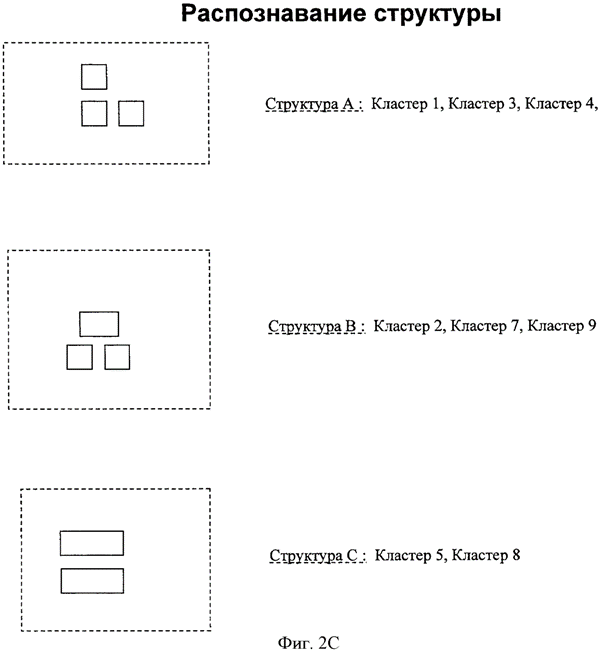
Следующий этап заключается в выполнении распознавания структуры для идентификации множества уникальных структур, существующих в модели ИС. В типичных моделях ИС те же структуры многократно повторяются в рамках одной модели. Распознавание конкретных уникальных структур позволяет средству EDA лишь выполнять обработку каждой уникальной структуры, одновременно воспроизводя результаты этой обработки или анализа для каждого повторяющегося случая с этими структурами в модели. Например, тогда как может существовать много миллионов разных многоугольников в модели ИС, эти миллионы многоугольников могут формировать только несколько тысяч уникальных структур. Вместо выполнения миллионов отдельных операций обработки для каждого многоугольника, только несколько тысяч уникальных структур требуют индивидуальной обработки в соответствии с исполнением настоящего изобретения.
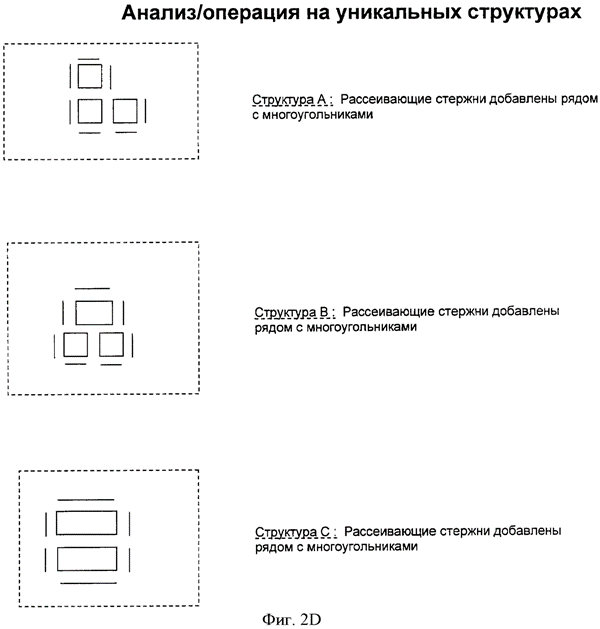
На фиг.2С кластеры 1-9, образованные из служащего образцом множества 200 многоугольников, были подвергнуты анализу, причем было установлено, что они представляют только три уникальные структуры внутри этих кластеров. В частности, структура
А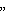 представляет собой уникальную компоновку из трех многоугольников, типичную для кластеров 1, 3, 4 и 6. Структура 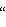В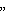 является уникальной компоновкой из трех многоугольников, типичной для кластеров 2, 7 и 9. Структура 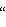С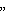 является уникальной компоновкой из двух многоугольников, типичной для кластеров 5 и 8.
Каждая из уникальных структур используется для выполнения требуемой обработки и(или) анализа. Например, представим себе, что желательно произвести обработку ОРС для добавления к модели рассеивающих стержней. На фиг.2D дан пример результатов добавления рассеивающих стержней к структуре А, структуре В и структуре С.
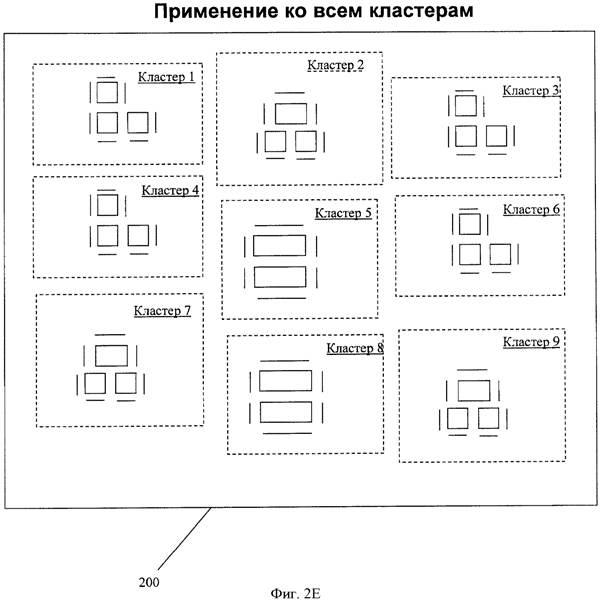
Что касается фиг.2Е, то следующий этап состоит в воспроизведении результатов обработки для каждой повторяющейся конкретизации уникальной структуры в кластерах. Таким образом, структур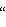а
А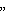 существует в кластерах 1, 3, 4 и 6. Поэтому комбинация рассеивающих стержней, установленная для структуры 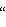А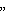, показанной на фиг.2D, повторяется для кластеров 1, 3, 4 и 6. Структура 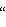В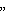 существует в кластерах 2, 7 и 9. Поэтому комбинация рассеивающих стержней, установленная для структуры 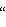В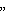, повторяется в кластерах 2, 7 и 9. Структура 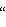С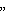 существует в кластерах 5 и 8. Аналогичным образом для других структур комбинация рассеивающих стержней, установленная для структуры 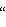С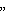, повторяется для кластеров 5 и 8.
Этот результат подчеркивает преимущества такого подхода. Вместо индивидуальной обработки каждого многоугольника в структуре или даже индивидуальной обработки каждого кластера обрабатываться будут только уникальные структуры. Повторяющееся использование этих структур позволяет однократный анализ/обработку уникальной структуры, но результаты такого анализа или обработки повторяются для каждой повторяющейся конкретизации этой структуры.
На этом этапе представляется полезным дать более подробное описание некоторых вариантов исполнения этого изобретения. Представим себе, что имеется данное число d и слой, включающий ряд многоугольников произвольной формы. Настоящее исполнение относится к множеству многоугольников, формирующих d-кластер, если для каждых двух многоугольников из множества существует последовательность многоугольников, где расстояние между любыми последовательными многоугольниками меньше или равно данному пороговому числу d. Два кластера эквивалентны, если имеет место ортогональная трансформация, создающая взаимно однозначное соответствие между многоугольниками из двух кластеров. Исполнение изобретения дает метод экстракции всех d-кластеров и кодирования d-кластера, что позволяет создать список представителей для всех классов эквивалентных d-кластеров, представленных в данном слое. Также, благодаря этому методу, из созданного списка можно определить тип эквивалентности любого экстрагированного d-кластера. Такой подход разрешает вышеописанные проблемы в O(n log n) времени и с помощью оперативной памяти O(n0,5).
Вклад нового метода состоит в разбиении данного слоя на трапеции. На основе фиг.3 представим себе, что многоугольник является трапецией с произвольным наклоном боковых ребер, заданным его вершинами с координатами (x1
d, уd), (x1u, уu), (xru, уu), (x1d, уd).
Пусть А=(x1, у1), В=(x2, у2) являются двумя вершинами. Этот метод, в соответствии с настоящим исполнением, вводит порядок ORD во множество всех вершин трапеции с помощью следующего правила:
вершина А<ORD вершины В, если 1) у1<у2 или 2) у1=у2 и x1
В таком подходе используется система представления SW (x1
d, уd), NW (x1u, уu), NE (xru, уu), SE (x1d, уd).
В соответствии с определенным исполнением для экстракции и формирования кластеров применяется метод
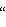прогонки на плоскости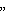. Процесс формирования кластера начинается с сортировки всех вершин входящих трапеций в возрастающем порядке ORD и их хранения в последовательном файле, обозначаемом в настоящем документе как FILE. В начале процесса каждая трапеция рассматривается как начало списка, что соответствует кластеру типа 1. В ходе процесса все трапеции получают числовые обозначения в соответствии с возрастающим порядком ORD своих юго-западных углов (SW). Далее, кластер типа 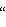к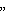, будет означать, что этот кластер содержит трапеции 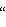к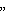 и что все трапеции, включенные в список, характеризуются как кластеры с указателями к оглавлению списка. Затем процесс начинается с высвечивания вершин из очереди FILE и проверки наличия уже рассматривавшихся трапеций в d-окрестности данной вершины, а также определении всех трапеций, которые отвечают этому условию.
Пусть h будет нижней границей ребра, рассматриваемой сейчас с помощью этого метода. Поскольку у каждой обнаруженной трапеции имеется указатель к головной части кластера, который ее содержит, то процесс может связать с каждой обнаруженной трапецией, от левой (юго-западный угол) и правой (юго-восточный угол) конечной точки р, последовательный номер содержащего его кластера. Затем процесс выбирает минимальное из этих чисел и назначает число трапеции
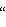А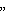. После этого процесс помещает (фактически, корень дерева) с помощью указателей к началу Вi списков (подкластеров), содержащих обнаруженные трапеции, и образует векторы (SW(A), SW(Bi)). Также в заголовке нового списка будет содержаться тип кластера - количество трапеций в кластере. Это вытекает из процесса, где кластер образует метод его кодирования.
Процесс будет представлять кластер как дерево. Каждый узел u дерева соответствует трапеции А(u) кластера. Благодаря процессу образования кластера, сын узла дерева соответствует головной части (корень поддерева) подкластера, образованного в ходе предыдущих этапов, и каждый узел содержит указатель к головной части кластера. Процесс кодирует каждый узел u дерева следующим образом:
полный код (l, (p1, (x1, у1), t1),
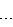, (p1, (x1, у1), t1)) и короткий код (l, (p1, f (x1, у1)), , (p1, f (x1, у1))),
где 1 является количеством сынов узла v, pi является указателем к головной части кластера, содержащей i-ю обнаруженную трапецию, (хi, уi) является вектором SWA(u) - SWA(сын u), следующим в возрастающем порядке номеров, соответствующих обнаруженным кластерам, ti является типом трапеции (координатами ее вершин), и функция f специально выбрана для усиления скорости распознавания кластеров.
Когда разница между координатой "у" рассматриваемой вершины и координатой "у" верхнего ребра трапеции, являющейся сейчас головной частью кластера, составляет больше чем d, то процесс образования этого кластера останавливается. В этот момент процесс проверяет, принадлежит ли только что сформированный кластер к уже обнаруженным кластерам эквивалентных d-кластеров, представленных в данном слое. Во-первых, процесс проводит сравнение короткого кода сформированного кластера с короткими кодами представителей классов эквивалентных d-кластеров, хранящихся в особом файле, а если короткие коды совпадают, то он проводит сравнение их полных кодов.
В конце процедуры процесс получает список представителей для всех классов эквивалентных d-кластеров, представленных в данном слое; любая трапеция включена в список трапеций, описывающих содержащий их кластер, и у любого такого списка имеется идентификация, содержащая его класс эквивалентности.
В соответствии с одним вариантом исполнения метод прогонки на плоскости может вести поиск только в горизонтальном или вертикальном направлении, поскольку сохраняет только объекты, пересекающие горизонтальную или вертикальную сканирующую строку во временной памяти (рабочий список). Для одновременного проведения обоих поисков используются два рабочих списка, обозначаемых как Текущая сканирующая строка (CSL) и Предыдущая граница (РВ).
CSL представляет собой рабочий список, управляемый с помощью уравновешенной структуры данных дерева. Каждый узел дерева данных содержит, в качестве ключа, линию, проходящую через боковое ребро под наклоном к одной вершине трапеции.
РВ хранит множество линейных сегментов границ трапеций, видимых вертикально со сканирующей строки. РВ управляется с помощью уравновешенной структуры дерева данных в возрастающем порядке координаты
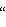х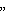, а листы указывают на соответствующие верхние горизонтальные или боковые сегменты трапеции или на НУЛЬ.
Каждый поиск и операция обновления (ввода или удаления) производится во время O(log k), где "k" представляет собой количество линейных сегментов в CSL и РВ. Сканированные вершины хранятся в очереди Q. Очередь Q поддерживает только те сегменты в списке РВ, где находится полоска d под текущей сканирующей строкой. Когда CSL меняет свое положение, т.е. координату "у", то тогда проверяется неравенство ycurr.vertex-yu>d для каждой вершины и от Q, и стирается сегмент h из РВ, если неравенство удерживается для каждой граничной вершины сегмента.
В одном исполнении значение расстояния d модифицируется для оптимизации процесса кластеризации. Причины этого заключаются в том, что если значение расстояния d является или слишком большим или слишком маленьким, то процесс может образовывать недостаточное количество кластеров и(или) недостаточное количество многоугольников, связанных с каждым кластером. Например, рассмотрим ситуацию, когда значение расстояния d является чрезмерно большим. В этом случае, вероятно, что будет иметься очень небольшое число кластеров, где каждый кластер потенциально обладает очень большим количеством многоугольников. Примером крайней ситуации является случай, когда значение d эквивалентно размеру всей ИС, и тогда процесс сформирует только отдельный кластер, связанный со всеми многоугольниками в ИС. С другой стороны, если значение расстояния d слишком мало, то здесь потенциально может быть слишком большое количество кластеров, где у каждого кластера имеется очень немного многоугольников.
Для решения этого вопроса, процесс должен быть конфигурирован для итерации с различными значениями для расстояния d. Одно или более пороговых значений может быть конфигурировано для идентификации точки, на которой идентифицируется приемлемый результат и итерации могут закончиться. В одном исполнении пороговые значения соответствуют (1) приемлемому или максимальному количеству многоугольников в кластере; и(или) приемлемому значению для d.
Например, процесс может начаться со сравнительно низким значением d. При высоком значении d вероятно, что будет иметь место сравнительно небольшое число кластеров, где у каждого кластера будет большое количество многоугольников. Этот результат сравнивается с установленной пороговой величиной (величинами). Если количество многоугольников в кластере (кластерах) превышает пороговое значение, то значение d уменьшается и снова происходит итерация процесса. Результирующее число многоугольников на один кластер снова сравнивается с пороговым значением для определения необходимости прекращения процесса. Если результаты превышают пороговое значение, то итерации повторяются до тех пор, пока не будет получен приемлемый результат. Один из способов уменьшения значения d в данном исполнении состоит в разделении d на установленный или расчетный коэффициент, например, разделить на 2.
Пороговое значение для расстояния d может применяться в соответствии с любым желаемым параметром. Например, пороговое значение для d может быть основано на правиле минимального расстояния между объектами в модели, т.е. с помощью установления порогового значения в 3 или 4 раза выше значения правила минимального расстояния между геометриями.
В отношении фиг.4 будет представлено более подробное описание метода распознавания кластером многоугольников.
На этапе 402 метод выполняет сортировку всех вершин входящих трапеций в возрастающем порядке ORD и хранит их в последовательном файле FILE. Каждая вершина несет информацию содержащей ее трапеции. Этот метод будет перечислять все трапеции в возрастающем порядке ORD, следуя правилу о том, что
трапеция А < трапеции В, если SW(A)
В начале процесс рассматривает каждую сквозную область как начало списка, соответствующее кластеру типа 1 (содержащему одну сквозную область; дальнейший кластер типа
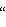k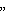 будет означать, что кластер содержит 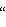k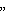 сквозных областей.
На этапе 403 делается определение о том, имеются ли еще вершины в FILE. Если в FILE имеются еще вершины, то метод на 404 выводит вершину v из FILE. Если в FILE больше нет вершин, то метод непосредственно переходит к этапу 412.
На этапе 406 делается определение в отношении неравенства:
уcurr.vertex-уu>d(*).
Если v является первой точкой в текущей сканирующей строке (координата "у" v > координаты "у" предшествующей точки), то необходимо проверить вышеуказанное неравенство относительно каждой вершины u из Q. Если неравенство (*) сохраняется для каждой граничной вершины сегмента из РВ, то метод стирает сегмент из РВ и обе граничные вершины сегмента из Q. Если вершина u типа NE (северо-восток) или NW (северо-запад), и для координаты "у" верхнего граничного ребра трапеции, являющейся головной частью кластера, содержащего текущую вершину u, неравенство (*) также сохраняется, то необходимо удалить и из Q и метод перейдет непосредственно к этапу 412.
На этапе 408, для каждой вершины v, метод используется для осуществления одной из следующих операций (4.1)-(4.4).
(4.1). Выполнить, когда v является юго-западным или юго-восточным углом: ввести боковое ребро с v в CSL. Определить (если расстояние меньше или равно d) ближайшее ребро с левой стороны v, если v является юго-западным углом, и с правой стороны от v, если v является юго-восточным углом, путем поиска CSL. Для каждого южного горизонтального ребра выполняющей трапеции проверить расстояние между горизонтальным ребром и всеми вершинами от РВ, лежащими под ребром. Также проверить расстояние между граничными вершинами горизонтального ребра и всеми сегментами от РВ, наклонными к вершинам, лежащим под ребром. Обнаружить (если расстояние меньше или равно d) сегменты из РВ, близкие к горизонтальному ребру, содержащему v. Ввести обе граничные вершины горизонтального ребра в РВ и удалить все вершины из РВ, лежащие между ними.
(4.2). Выполнить, если v является юго-западным углом, и затем для каждого сегмента f из рабочего списка РВ, где имеется, по крайней мере, один торец и, следовательно,
координата "х" v - координата "х"<=d.
Проверить, если эвклидово расстояние между v и сегментом f меньше или равно d.
Определить, является ли расстояние равным <=d.
Если v является юго-восточным углом, то для каждого сегмента из рабочего списк
