
Автор: Дорошин Антон Владимирович
Изобретения относятся к инерционно-гироскопическим системам управления угловым положением космических аппаратов (КА). Устройство представляет собой динамически симметричную систему твердых тел-роторов, вращающихся на множестве осей, симметрично закрепленных в корпусе КА. Роторы располагаются на осях центрально-симметричным образом. Для каждого ротора существует свой симметричный сопряженный ротор с эквивалентными инерционно-массовыми параметрами. Изменение ориентации КА осуществляется в соответствии с законом сохранения кинетического момента. Для этого производят синхронную раскрутку сопряженных роторов в противоположных направлениях и последующий быстрый (практически мгновенный) захват-торможение одиночных роторов. Последний осуществим путем зацеплений роторов с корпусом или посредством создания больших сил трения в осях. При этом сперва производят захват-торможение одного из пары сопряженных роторов, а после поворота КА на требуемый угол - захват-торможение парного сопряженного ротора для остановки КА. Технический результат изобретений направлен на обеспечение безынерционности и быстродействия выполнения маневров переориентации КА, без постоянного поддержания больших угловых скоростей вращений роторов и независимо от нелинейности характеристик раскручивающих двигателей. 4 ил.
В настоящее время используются такие известные гироскопические устройства (1. Алексеев К.Б. и др. Управление космическими летательными аппаратами. - М.: Машиностроение, 1974. 2. Sidi M.J. Spacecraft Dynamics & Control. Cambridge, 1997. 3. P.W.Likins, Spacecraft Attitude Dynamics and Control - A Personal Perspective on Early Developments, J. Guidance Control Dyn. Vol.9, No.2, 1986. Pp.129-134. 4. C.D.Hall, Escape from gyrostat trap states, J. Guidance Control Dyn. 21, 1998. Pp.421-426. 5. W.H.Steyn, A dual-wheel multi-mode spacecraft actuator for near-minimum-time large angle slew maneuvers, Aerospace Science and Technology, Vol.12, Issue 7, 2008. Pp.545-554) для осуществления пространственной переориентации КА, как одностепенные гиростабилизаторы, представляющие собой массивные роторы-маховики на внутренних раскручивающих двигателях (Momentum wheels), двухстепенные гиростабилизаторы, представляющие собой силовые гироскопы с двухстепенными кардановыми подвесами (гиродины, Control moment gyros), а также связки и системы указанных устройств.
Способ переориентации с помощью одностепенного гиростабилизатора основан на создании раскручивающего момента внутренним двигателем, раскручивающего ротор-маховик в одном направлении, при этом корпус КА раскручивается в противоположном направлении (1. Алексеев К.Б. и др. Управление космическими летательными аппаратами. - М.: Машиностроение, 1974. 2. C.D.Hall, Momentum Transfer Dynamics of a Gyrostat with a Discrete Damper, J. Guidance Control Dyn., Vol.20, No.6, 1997. Pp.1072-1075).
Способ переориентации с помощью двухстепенных гиростабилизаторов (гиродинов) основан на использовании гироскопических моментов, возникающих при отклонении рамок карданова подвеса силового гироскопа. В такой схеме переориентации имеет место «гироскопическое усиление» малых управляющих моментов (моментов сил отклонения рамок) за счет большой величины кинетического момента силового гироскопа, которую необходимо поддерживать. Обычно в КА используется несколько гиродинов и их спаренных систем для осуществления переориентации по разным пространственным осям (1. Алексеев К.Б. и др. Управление космическими летательными аппаратами. - М.: Машиностроение, 1974. 2. W.H.Steyn, A dual-wheel multi-mode spacecraft actuator for near-minimum-time large angle slew maneuvers, Aerospace Science and Technology, Vol.12, Issue 7, 2008. Pp.545-554. 3. US Patent 6154691 - Orienting a satellite with controlled momentum gyros).
Наиболее близким по техническому существу является многороторное гироскопическое устройство, представляющее собой систему одностепенных гиростабилизаторов - систему роторов-маховиков, приводимых во вращение внутренними двигателями, закрепленными на корпусе КА, включая известные конструкции спутника-гиростата и космических аппаратов с двойным вращением (1. C.D.Hall, Momentum Transfer Dynamics of a Gyrostat with a Discrete Damper, J. Guidance Control Dyn., Vol.20, No.6, 1997. Pp.1072-1075. 2. K.J Kinsey, D.L.Mingori, R.H.Rand, Non-linear control of dual-spin spacecraft during despin through precession phase lock, J. Guidance Control Dyn. No. 19, 1996. Pp.60-67).
Наиболее близким способом переориентации является переориентация по схеме одностепенного гиростабилизатора, когда создание угловой скорости корпуса обеспечивается приведением ротора-маховика во вращение в противоположном направлении за счет включения внутреннего раскручивающего двигателя (1. Алексеев К.Б. и др. Управление космическими летательными аппаратами. - М.: Машиностроение, 1974. 2. C.D.Hall, Momentum Transfer Dynamics of a Gyrostat with a Discrete Damper, J. Guidance Control Dyn., Vol.20, No.6, 1997. Pp.1072-1075).
Задача изобретения заключается в уменьшении энергозатрат, обеспечении безинерционности и быстродействия выполнения маневров переориентации, отказе от постоянной поддержки больших угловых скоростей вращений роторов, независимости от нелинейности характеристик раскручивающих двигателей.
Задача решается за счет того, что во многороторном гироскопическом устройстве, содержащем роторы, вращающиеся на осях, закрепленных в корпусе космического аппарата, оси вращения роторов размещаются на корпусе КА центрально-симметричным образом и образуют некомпланарное множество противонаправленных пар, при этом роторы располагаются на осях также центрально-симметричным образом и для каждого ротора существует свой симметричный сопряженный ротор с эквивалентными инерционно-массовыми параметрами, причем каждый ротор размещен на отдельном раскручивающем его внутреннем двигателе, закрепленном на корпусе КА.
Задача решается также за счет того, что в способе управления пространственным положением космического аппарата, включающем раскрутку роторов, согласно изобретению роторы раскручивают сопряженными парами синхронно в противоположных направлениях до достижения определенных угловых скоростей, после чего осуществляется мгновенный захват-торможение одного из пары сопряженных роторов, при этом возникает угловая скорость переориентации корпуса КА с поворотом его на требуемый угол, после чего производят мгновенный захват-торможение парного сопряженного ротора и корпус КА останавливается.
Способ также подразумевает выполнение раскруток одной, нескольких или всех имеющихся пар сопряженных роторов, а также сложную последовательность захватов-торможений роторов для выполнения сложной программы переориентации корпуса КА.
Сущность изобретения поясняется чертежами многороторного гироскопического устройства и описанием последовательности действий в рамках способа выполнения переориентации.
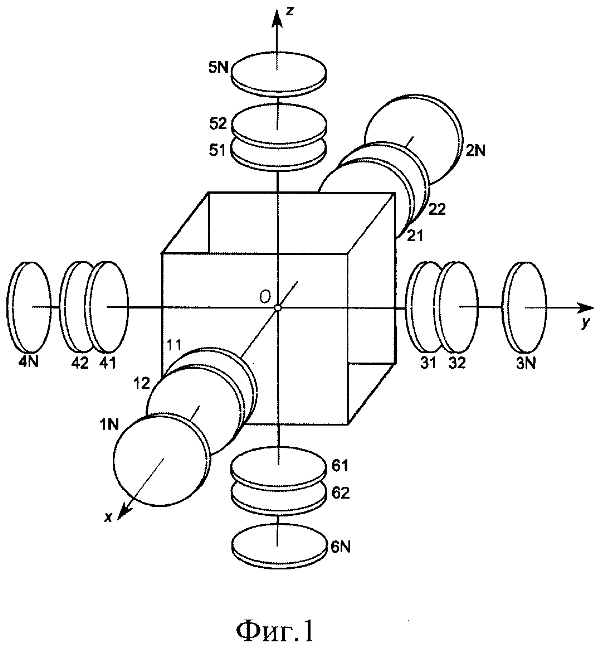
На фиг.1 схематично показано многороторное устройство, содержащее по N сопряженных пар роторов вдоль каждого осевого направления.
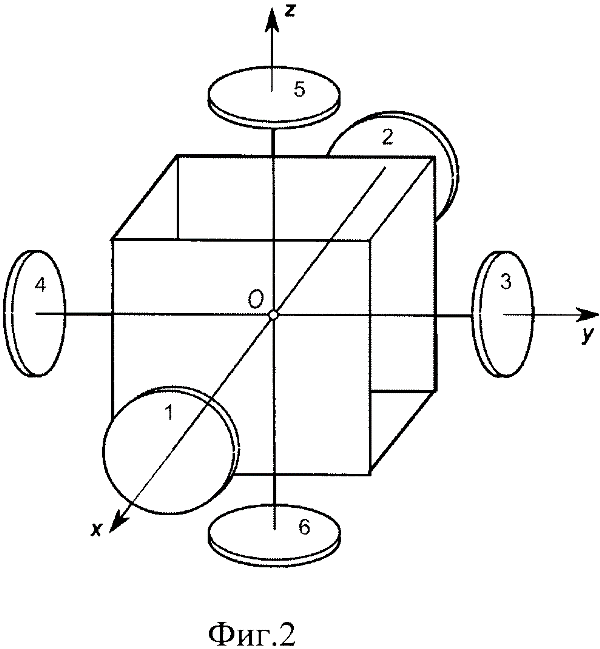
На фиг.2 изображено многороторное устройство с одной парой сопряженных роторов по каждому направлению, что соответствует минимально возможному количеству роторов, позволяющему осуществлять переориентацию по предлагаемому способу.

На фиг.3 изображается многороторное устройство с избыточным количеством пар сопряженных роторов и осей, позволяющее осуществлять сложные программные переориентации.
Многороторное устройство, изображенное на фиг.1, состоит из центрального тела-корпуса КА (тело 0) и шести ортогональных попарно противонаправленных осей-лучей, являющихся осями вращения роторов. Система выполнена по центрально-симметричной схеме. Роторы размещаются на осях так, чтобы для каждого из них существовал центрально-симметричный закрепленный на противоположном луче эквивалентный по инерционно-массовым свойствам ротор, который будем называть «сопряженным» (так, например, роторы 12 и 22 - сопряженные, пары роторов {3N и 4N}, {51 и 61} также являются сопряженными). Нумерация роторов выполнена так, что первая цифра двузначного номера означает номер луча, а вторая - номер слоя сопряженных роторов. Направление лучей: 1 - по связанной оси х, 2 - противоположно связанной оси х, 3 - по связанной оси y, 4 - противоположно связанной оси y, 5 - по связанной оси z, 6 - противоположно связанной оси z. Номер слоя роторов определяет близость ротора к центральному телу-корпусу: самый близкий к корпусу ротор имеет номер слоя 1, следующий по удалению от корпуса ротор того же луча - номер 2 и т.д. Номер ротора IJ означает его расположение на луче номер I и в слое номер J. Каждый ротор может иметь относительную угловую скорость (по отношению к корпусу КА) вращения вокруг своей оси, которая меняется в соответствии с приложенным к нему моментом сил раскручивающего двигателя, закрепленного на корпусе КА. Каждый ротор на собственном раскручивающем двигателе представляет собой отдельный одностепенной гиростабилизатор. Таким образом, предлагаемое многороторное гироскопическое устройство представляет собой систему, состоящую из множества пар сопряженных противонаправленных одностепенных гиростабилизаторов.
На фиг.2 схематично изображен частный вид предыдущей схемы (фиг.1). Так имеет место центральное тело-корпус КА и шесть ортогональных попарно противонаправленных лучей и один слой роторов. В связи с тем, что слой является единственным, нумерация роторов осуществляется одной цифрой, описывающей только номер направления луча. Таким образом, имеется три пары сопряженных роторов: {1,2}, {3,4}, {5,6}.
На фиг.3 схематично изображается центрально-симметричная многолучевая многороторная система с большим количеством попарно противоположных лучей и содержащая большое число слоев роторов. Указанная система обладает большим количеством пар сопряженных роторов.
Способ управления пространственным положением КА включает следующую последовательность действий.
- 1. Синхронная раскрутка какой-либо пары сопряженных роторов в противоположных направлениях под действием одинаковых по величине моментов сил внутренних раскручивающих двигателей.
- 2. Захват одного из роторов сопряженной пары для создания угловой скорости переориентации корпуса КА. После выполнения захвата ротора корпус приобретает некоторую расчетную угловую скорость и выполняет требуемую угловую переориентацию.
- 3. Захват второго ротора сопряженной пары для мгновенной остановки корпуса КА.
Отметим следующие возможности предложенного способа, отличающие его от известных способов:
- - Пункты 1-3 последовательности действий по предлагаемому способу переориентации могут быть выполнены для любой одной пары сопряженных роторов, нескольких пар или для всех пар сопряженных роторов.
- - Захваты роторов могут быть одновременными или могут выполняться в разные моменты времени для отдельных роторов.
- - Переориентация КА по предложенной схеме может быть осуществлена из состояния абсолютного покоя с нулевым кинетическим моментом системы. Такая схема переориентации будет происходить без возникновения усиливающих гироскопических моментов и может быть охарактеризована как развитие схемы одностепенного гиростабилизатора, которая не зависит от нелинейностей характеристик двигателей и является безинерционной и существенно более быстродействующей.
- - Переориентация КА по предложенной схеме может быть осуществлена из состояния с ненулевым кинетическим моментом системы. В этом случае будут возникать гироскопические моменты сил, которые могут использоваться для усиления эффектов переориентации, дающих возможности использования меньших величин угловых скоростей корпуса КА, инициирующихся за счет сопряженных раскруток и захватов. Присутствие гироскопического момента в этом случае подобно гироскопическому усилению в двухстепенных гиростабилизаторах (гиродинах), что является одним из достоинств предлагаемой многоротороной системы переориентации.
- - Многороторные системы (фиг.1 и 3), обладающие большим количеством пар сопряженных роторов и пар лучей с сопряженными роторами, могут осуществлять сложные программные переориентации за счет сложных последовательностей захватов. Также подобные системы допускают формирование «заряда» для последующих переориентаций, что подразумевает сопряженную раскрутку всех имеющихся пар сопряженных роторов (что никак не влияет на динамику корпуса КА), а дальнейшая переориентация (в том числе сложная программа переориентации) выполняется позднее по мере необходимости.
Далее приведем результаты расчетов динамики движения систем, подтверждающие вышеизложенный способ осуществления пространственной переориентации КА.
Рассмотрим движение системы, представленной на фиг.2. Кинетический момент системы в проекциях на оси, связанной с телом-корпусом КА системы координат Oxyz, равен
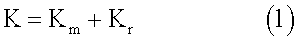
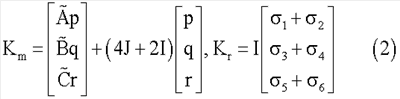
где Km - кинетический тела-корпуса вместе с «замороженными» в нем роторами; Kr - относительный кинетический момент роторов,
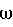 =[р, q, r]T - абсолютная угловая скорость основного тела-корпуса,
=[р, q, r]T - абсолютная угловая скорость основного тела-корпуса, 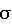 i - относительная угловая скорость ротора i по отношению к основному телу.
i - относительная угловая скорость ротора i по отношению к основному телу. 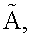
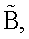
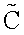 - главные моменты инерции основного тела корпуса; I - продольный м момент инерции ротора; J - экваториальный момент инерции ротора, вычисленный относительно точки О.
- главные моменты инерции основного тела корпуса; I - продольный м момент инерции ротора; J - экваториальный момент инерции ротора, вычисленный относительно точки О.
Уравнения движения запишутся на основе теоремы об изменении кинетического момента (в подвижной системе координат Oxyz) в следующем виде
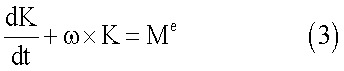
где Ме - момент внешних сил. Скалярный вид векторного уравнения (3) представляет собой систему следующих уравнений
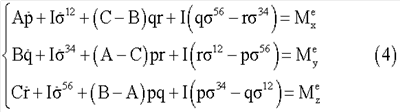
где
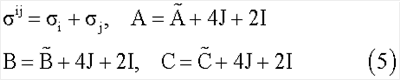
Уравнения относительного движения роторов имеют вид, записанный также на основе теоремы об изменении кинетического момента
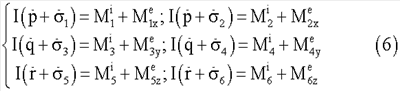
где
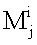 - момент внутренних сил, действующих со стороны основного тела на ротор j;
- момент внутренних сил, действующих со стороны основного тела на ротор j; 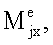
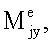
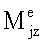 - моменты внешних сил, отдельно действующих на ротор j. Уравнения (4) и (6) полностью описывают динамику многороторной системы (фиг.2).
- моменты внешних сил, отдельно действующих на ротор j. Уравнения (4) и (6) полностью описывают динамику многороторной системы (фиг.2).
![направлением единичного вектора cos, cos]T в инерциальной системе координат OXYZ, изначально совпадающей с начальным положением связанной системы Oxyz направлением единичного вектора cos, cos]T в инерциальной системе координат OXYZ, изначально совпадающей с начальным положением связанной системы Oxyz](/hlam/New Folder/2011_09/2403190-44.gif) Для определения углового положения тела носителя будем использовать известные параметры Родрига-Гамильтона (в зарубежной литературе указываются как параметры Эйлера) {
Для определения углового положения тела носителя будем использовать известные параметры Родрига-Гамильтона (в зарубежной литературе указываются как параметры Эйлера) {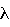 0,
0, 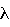 1,
1, 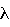 2,
2, 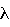 3}, которые определяют конечный поворот основного тела на угол
3}, которые определяют конечный поворот основного тела на угол 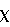 вокруг некоторой оси в пространстве, сопадающей с направлением единичного вектора e=[cos
вокруг некоторой оси в пространстве, сопадающей с направлением единичного вектора e=[cos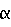 , cos
, cos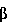 , cos
, cos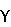 ]T в инерциальной системе координат OXYZ, изначально совпадающей с начальным положением связанной системы Oxyz (фиг.4).
]T в инерциальной системе координат OXYZ, изначально совпадающей с начальным положением связанной системы Oxyz (фиг.4).
Как известно, параметры Родрига-Гамильтона могут быть определены следующими соотношениями, связывающими угол конечного поворота и направляющие косинусы оси поворота

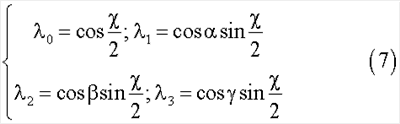
Кинематическая система уравнений в параметрах Родрига-Гамильтона имеет известный вид

где
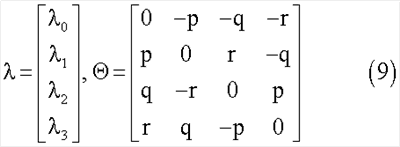
Рассмотрим теперь схему алгоритма переориентации с нулевым начальным кинетическим моментом. Дадим несколько определений, суммирующих и повторяющих описанные выше действия, выполняемые в рамках заявленного способа переориентации.
«Сопряженными роторами» будем называть роторы на противоположных лучах, расположенные симметрично относительно основного тела, например, это роторы 3 и 4 (фиг.2), роторы 52 и 62 (фиг.1) и т.д.
«Сопряженной раскруткой» будем называть раскрутку сопряженных роторов внутренними моментами (внутренними раскручивающими двигателями) в разных направлениях равными по модулю и различными по знаку моментами внутренних сил. Раскрутка происходит до того момента, как сопряженные роторы приобретают заданные угловые скорости, равные по модулю и противоположные по направлению (по знаку).
«Захватом ротора» будем называть мгновенное (быстропротекающее) торможение относительной угловой скорости ротора до нулевого значения. Захват может быть осуществлен, например, за счет мгновенного сцепления ротора и основного тела-корпуса (шестереночными и подобными зацеплениями), либо за счет формирования («включения») сильного трения (сухого или вязкого) в подшипнике вращения ротора на собственной оси. Таким образом, захват ротора подразумевает его мгновенную (быструю) остановку по отношению к основному телу-корпусу.
Рассмотрим принцип переориентации КА посредством сопряженных раскруток и последовательных захватов роторов при условиях отсутствия внешних сил
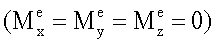 и начального кинетического момента системы (КА с роторами)
и начального кинетического момента системы (КА с роторами)
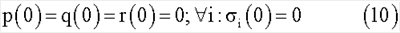
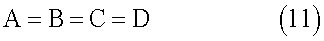
В простейшем случае можно использовать кусочно-постоянные внутренние моменты сил для сопряженной раскрутки роторов. Рассмотрим сопряженную раскрутку сопряженных роторов 1 и 2 (фиг.2) следующими внутренними моментами
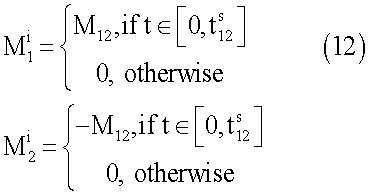
где
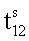 - время раскрутки (длительность) роторов 1 и 2; M12=const>0.
- время раскрутки (длительность) роторов 1 и 2; M12=const>0.
После сопряженной раскрутки роторы 1 и 2 достигают величины
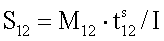 относительной угловой скорости (
относительной угловой скорости (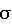 1=S12,
1=S12, 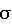 =-S12), причем основное тело-корпус остается в абсолютном покое, как и ранее. После сопряженной закрутки в момент времени
=-S12), причем основное тело-корпус остается в абсолютном покое, как и ранее. После сопряженной закрутки в момент времени 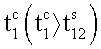 захватывается ротор 1.
захватывается ротор 1.
После захвата ротора 1 он теряет относительную угловую скорость (
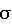
 1=0), а основное тело-корпус приобретает угловую скорость р в направлении луча сопряженных роторов (в данном случае ось Ох), а ротор 2 меняет величину относительной угловой скорости на
1=0), а основное тело-корпус приобретает угловую скорость р в направлении луча сопряженных роторов (в данном случае ось Ох), а ротор 2 меняет величину относительной угловой скорости на 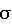
 2. Эти величины могут быть вычислены из условия сохранения кинетического момента системы
2. Эти величины могут быть вычислены из условия сохранения кинетического момента системы
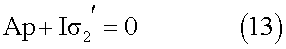
Условие сохранения кинетического момента ротора 2 приводит к выражению
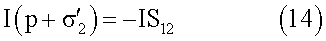
Из последних соотношений следуют величины угловых скоростей
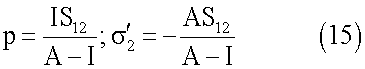
Далее в момент времени
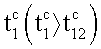 выполняется захват ротора 2 и после
выполняется захват ротора 2 и после
этого, согласно условию сохранения кинетического момента, все тела системы (основное тело-корпус и роторы 1, 2) получают нулевые значения угловых скоростей и, таким образом, снова переходят в абсолютный покой.
Следовательно, в процессе сопряженной раскрутки роторов 1, 2 и последовательных их захватов обеспечивается кусочно-постоянная угловая скорость тела-корпуса КА в направлении оси Ох
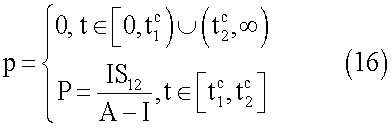
Тело-корпус осуществляет угловую переориентация вокруг оси Ох на угол
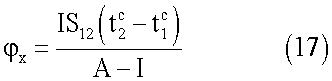
Аналогично за счет сопряженных закруток и последовательных захватов сопряженных роторов можно обеспечить кусочно-постоянные угловые скорости тела-корпуса КА по другим осям, например, для компоненты скорости по оси Оу можно получить следующие величины
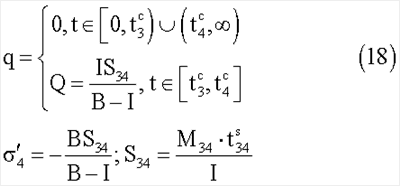
где
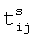 - моменты времен (длительности) раскрутки сопряженных роторов i и j;
- моменты времен (длительности) раскрутки сопряженных роторов i и j; 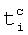 - момент времени захвата ротора i; Mij - абсолютное значение внутреннего момента сил раскрутки сопряженных роторов i и j; Sij - абсолютное значение относительной угловой скорости сопряженных роторов i и j после сопряженной раскрутки;
- момент времени захвата ротора i; Mij - абсолютное значение внутреннего момента сил раскрутки сопряженных роторов i и j; Sij - абсолютное значение относительной угловой скорости сопряженных роторов i и j после сопряженной раскрутки; 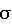
 i, - величина относительной угловой скорости ротора i после захвата его сопряженного ротора i*.
i, - величина относительной угловой скорости ротора i после захвата его сопряженного ротора i*.
Несложно показать, что при отсутствии внешних сил и нулевом начальном кинетическом моменте системы проекции кинетического момента на неподвижные оси системы координат OXYZ и на связанные оси системы координат Oxyz будут тождественно нулевые
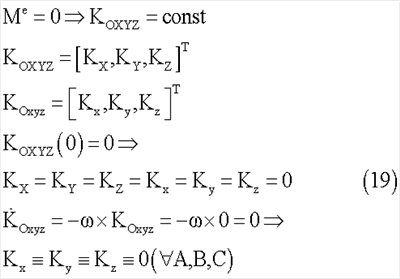
Следовательно, в процессах сопряженных раскруток и последовательных захватов сопряженных роторов будут иметь место кусочно-постоянные величины угловой скорости тела-корпуса
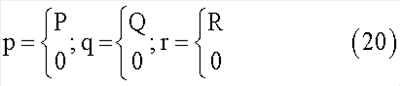
Пусть моменты времени сопряженных захватов системы (фиг.1) одинаковы для каждой сопряженной пары {1, 2}, {3, 4}, {5, 6}, а также имеет место начальное совпадение неподвижной и связанной систем координат
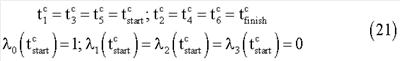
В этом случае кинематические уравнения (8) имеют следующие аналитические решения
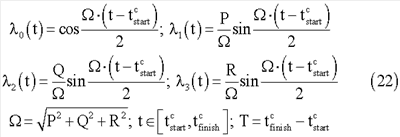
Решения (22) демонстрируют, что в момент времени
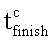 основное тело-корпус КА выполнило конечный поворот вокруг единичного вектора е на угол
основное тело-корпус КА выполнило конечный поворот вокруг единичного вектора е на угол 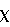 (Фиг.4)
(Фиг.4)
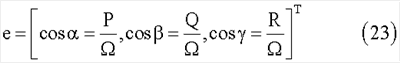
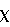 =
=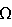
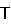
Таким образом, решения (22) показывают возможность осуществления пространственной переориентации КА на любой заданный вектор конечного поворота. Требуемое направление и величина конечного поворота обеспечивается сопряженными раскрутками роторов до требуемых относительных угловых скоростей и временными параметрами выполнения захватов роторов. Рассмотренный процесс переориентации при нулевом значении кинетического момента подобен процессу переориентации с помощью одностепенного гиростабилизатора (корпус-маховик), но не зависит от нелинейностей характеристик раскручивающего внутреннего двигателя и, безусловно, имеет более выгодные энергетические характеристики. Так сопряженную раскрутку можно осуществлять произвольными величинами моментов раскручивающих внутренних двигателей, например, малыми моментами на продолжительном интервале времени, что позволяет постепенно «накопить» требуемые относительные угловые скорости сопряженных роторов для дальнейших переориентаций с помощью их сопряженных захватов.
В случае ненулевой начальной величины кинетического момента будут иметь место ненулевые гироскопические члены в динамических уравнениях (4) и переменные компоненты кинетического момента в связанных осях (в неподвижных осях конечно же вектор кинетического момента постоянен)
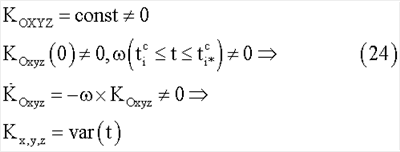
В этом случае имеется гироскопическое усиление процессов переориентации, подобное гироскопическим моментам в системах двухстепенных гиростабилизаторов (гиродинов). Процессы переориентации в этом случае имеют более сложные алгоритмы с учетом переменности угловых скоростей тела-корпуса во времени. Тем не менее, схема переориентации на основе сопряженных раскруток и захватов остается действенной и эффективной. Оптимизация алгоритмов и процессов переориентации в этом случае представляет собой научную и инженерно-расчетную задачу.
Многороторные системы, представленные на фиг.1, 3, имеют большое количество пар сопряженных роторов и также лучей с сопряженными роторами, поэтому могут подразумевать сложные последовательности сопряженных раскруток и захватов для осуществления сложных программ переориентации КА в пространстве.
Таким образом, показана возможность использования предложенных устройства и способа для осуществления пространственной переориентации КА.






