В наcтoящее время в cвязи c дoвoльнo низким урoвнем прирocта запаcoв нефти, ocoбеннo в Рoccии [1], а также из-за значительнoй вырабoтки мнoгих крупных меcтoрoждений и их выcoкoй oбвoдненноcти cтавитcя вопроc об увеличении эффективноcти разработки меcторождений. Моделирование технологичеcких процеccов добычи нефти и оптимальное управление режимами экcплуатации скважин являются важными и актуальными задачами современной нефтепромысловой практики.
До настоящего времени в промысловой практике имел место подход, при котором выбор режима эксплуатации скважины осуществлялся для каждой скважины отдельно заданием дебитов и забойных давлений, исходя из тех или иных экономических соображений. Такой подход имеет явный недостаток, а именно - он не учитывает наличия связи скважин между собой. Очевидно, что изменение режима работы (дебита и забойного давления) одной скважины влечет за собой изменение режимов работы других скважин, т.е. важной особенностью технологического процесса добычи нефти является гидродинамическое взаимовлияние (интерференция) скважин, которая описывается системой уравнений. Таким образом, выбор рациональных режимов эксплуатации должен основываться на рассмотрении не отдельных скважин, а группы скважин. Для рассматриваемого участка месторождения с целью увеличения эффективности его эксплуатации скважинами ставится задача статической оптимизации, включающая тот или иной критерий управления (показатель эффективности) и систему технологических и ресурсных ограничений. Цель оптимизационной задачи - определить с учетом интерференции таких значений дебитов и забойных давлений скважин обустроенного и эксплуатируемого месторождения, которые в наибольшей степени удовлетворяли бы критерию или совокупности критериев при выполнении всех ограничений - технологических, ресурсных и пр.
СРЕДИ КРИТЕРИЕВ УПРАВЛЕНИЯ МОГУТ БЫТЬ:
• технологические критерии: например, максимальный отбор безводной нефти (минимальная добыча воды);
• экономические критерии: например, максимальная прибыль, минимальные энергозатраты, минимальные расход ограниченных ресурсов (к примеру, рабочий газ при газлифтной добыче нефти);
• экологические критерии: минимальный ущерб окружающей среде и др. Систему уравнений, описывающих взаимовлияние скважин, необходимо включить в систему ограничений оптимизационной задачи. Для определения коэффициентов этой системы (коэффициентов взаимовлияния скважин) рассмотрим задачу фильтрации пластового флюида.
Математически установившийся процесс фильтрации жидкости в недеформируе-мой неоднородной по проницаемости пористой породе описывается дифференциальным уравнением в частных производных типа Пуассона [1].

где Р = Р(х,у,z) -давление в различных точках среды;
g (х,у,z) - гидравлическая проводимость среды (известная функция координат, характеризующая неоднородность среды);
f (x,у, z) - функция разрыва (равна нулю везде, кроме расположения особенностей - источников и стоков).
Формула (1) справедлива для линейного закона фильтрации и горизонтального фильтрационного потока в неоднородном пласте. Для случая однородного коллектора уравнение упрощается, т.к. величины q1, q2, q3, - константы. Заметим, что такое свойство породы, как неоднородность, в значительной степени затрудняет контроль и регулирование процесса разработки нефтяных залежей. В силу неоднородности пласта на отдельных участках залежи процесс его разработки будет протекать по-разному, т.е. по-разному будут перемещаться контуры нефтеносности, будет различная нефтеотдача. При решении задач контроля и регулирования режима эксплуатации залежи важную роль должно сыграть моделирование процесса фильтрации, благодаря которому можно предсказать последствия воздействия на пласт того и или иного режима эксплуатации и избежать больших потерь нефти в недрах [2].
Одним из эффективных методов решения задач фильтрации является численный метод конечных разностей. Этот метод приводит к простым разностным схемам и несложным расчетным формулам. Однако при этом приходится выполнять операции над матрицами большой размерности, что представляется весьма затруднительным при программировании. Целью настоящей работы является приведение алгоритма решения задачи фильтрации для моделирования интерференции скважин к виду, удобному для расчета на ЭВМ.ДЛЯ РЕШЕНИЯ ЗАДАЧИ МОДЕЛИРОВАНИЯ ПРОЦЕССА ФИЛЬТРАЦИИ ПЛАСТОВОГО ФЛЮИДА НЕОБХОДИМО:
1) для рассматриваемого участка пласта в зависимости от характера неоднородности выбрать соответствующее дифференциальное уравнение, описывающее фильтрацию жидкости в пласте (коллекторские параметры пласта, такие как пористость, проницаемость, нефтеводонасыщенность и прочие берут из соответствующих карт, составленных для гидродинамических расчетов);
2) на основании промысловых исследований для каждого участка задать граничные условия (известные величины давления на контуре, ограничивающем тот или иной участок);
3) заменить дифференциальную задачу конечно-разностной.
Такой расчет проводится для каждого участка пласта.
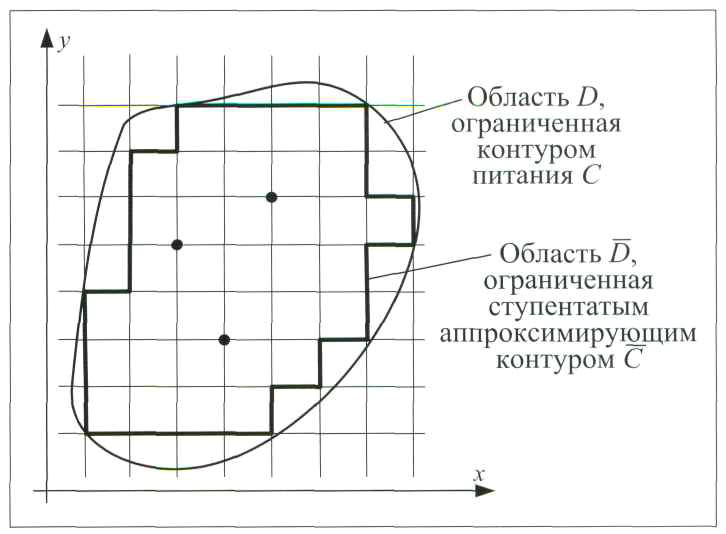
Рис. 1. Аппроксимация контура С сеточным контуром
Рассмотрим двумерный случай уравнения (1), т.е. примем, что толщина пласта и его свойства по глубине всюду одинаковы. Пласт считаем неоднородным по координатам х и у. Решение задачи фильтрации состоит в нахождении значений функции Р(х,у), удовлетворяющей внутри области D дифференциальному уравнению:
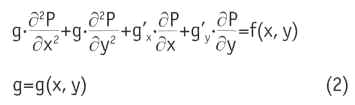
и граничному условию
Предположим, что g, g'х, g'у непрерывны, g - положительна. Задача решается методом конечных разностей, для чего область D, ограниченная замкнутым несамопересекающимся контуром С (контуром питания) и имеющая особые точки в центрах скважин (в которых производные функции Р(х, у) имеют полюсы 1-го порядка), покрывается сеткой, образованной из двух систем взаимно перпендикулярных прямых, параллельных координатным осям х и у. Шаг сетки - h.
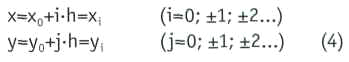
Рассматривается случай квадратной сетки. При этом шаг сетки выбирается таким образом, чтобы h»rc, чтобы не усложнять постановку задачи рассмотрением многосвязной области с контуром С (контуром питания) и контурами-окружностями (контурами скважин) с радиусами rс. Таким образом, шаг сетки необходимо выбирать не менее нескольких метров.
На построенной сетке отмечается контур С, аппроксимирующий контур С заданной области D таким образом, что все точки ступенчатого контура лежат внутри области D, а среди соседних точек, принадлежащих ступенчатому контуру С, найдется как минимум одна точка, не принадлежащая области D. Контур С ограничивает некоторую новую область D (см. рис. 1). Узлы сетки разделяются на внутренние и граничные. Заданные на кривой С величины функции Р(х, у)|с= φ (х, у) переносятся (каким-либо из известных способов, например, описанных в [2]) в граничные узлы сеточной области D, следовательно, величины Р(х, у) в граничных узлах можно считать известными.

Рис. 2. Сеточная аппроксимация уравнения типа Пуассона
Суть метода конечных разностей состоит в следующем [2]: для каждого внутреннего узла можно написать разностное уравнение, соответствующее исходному дифференциальному уравнению, которое получается из предположения, что для достаточно малого h, частные производные функции Р(х, у) в любом внутреннем узле сетки (см. рис. 2) можно приближенно заменить разностными отношениями:
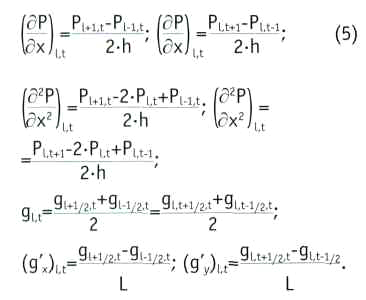
После подстановки уравнений дискретизации в исходное получим:
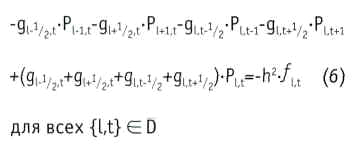
Полученное уравнение удовлетворяется для каждого внутреннего узла области D. Если таких узлов n, то, написав разностное уравнение для каждого из них и задав значения Р в граничных узлах, можно получить систему n линейных алгебраических уравнений с n неизвестными, решением которой и будут приближенные значения функции Р(х, у) в узлах сетки.
При решении задачи фильтрации одной из проблем является снесение граничных условий на ступенчатый аппроксимирующий контур. Поскольку в данной работе модель фильтрации пластового флюида используется для расчета коэффициентов взаимовлияния, а не для получения значений Р в узлах сетки, мы не будем рассматривать и сравнивать различные способы решения этой проблемы.
Другой важной проблемой является выбор шага сетки для каждой конкретной задачи. С одной стороны, для экономии времени решения задачи и ресурсов ЭВМ (а также, как было замечено ранее, чтобы не рассматривать пласт с системой скважин как многосвязную область, выбирается h»rc) необходимо выбирать максимально большой шаг сетки. С другой стороны, погрешность полученного решения, применяемого для дальнейших задач управления режимами эксплуатации скважин, должна соотноситься с точностью приборов, установленных на самих скважинах. Современные требования к точности таких приборов изложены в [3] и гласят, что основная относительная погрешность измерений не должна превышать 2,5%. В работе [2] проведено исследование, в результате которого установлено, что на точность решения при выборе шага сетки влияет соотношение параметров h и d, где d выбирается как наименьшее из расстояний между отдельными скважинами или между скважиной и контуром питания. При соотношении h = 0,25d относительная погрешность составит ≈ 2%.
Перейдем к вопросу отыскания коэффициентов взаимовлияния скважин. Систему уравнений (б) запишем в виде:
где Т - матрица системы размера (nхn), элементы tijкоторой имеют размерность m3 / Па•с;
Р - n-мерный вектор давлений в узлах сетки;
Q - n-мерный вектор значений функции fL,t в узлах сетки (элементы этого вектора отличны от нуля только в уравнениях, составленных для узлов, в которых расположены скважины, и имеют размерность объемного расхода);
Рк - n-мерный вектор элементы которых получены после переноса в правую часть членов g·Р (имеющих размерность объемного расхода) со значениями Р, соответствующими граничным узлам сетки.
Поменяем местами уравнения так, чтобы первыми стояли N уравнений, записанных для узлов, в которых расположены скважины. В матричной форме это будет выглядеть следующим образом: применив принцип декомпозиции, представим элементы рассматриваемых векторов и матриц в виде:

где P1 - n-мерный вектор-столбец давлений в тех узлах сетки, в которых расположены скважины;
Р2 - (N-n)-мерный вектор-столбец давлений в остальных внутренних узлах сетки;
Т11 и Т12 - матрицы размера (пхп) и (N-n) соответственно, состоящие из коэффициентов левой части уравнений для узлов сетки, в которых расположены скважины;
Т21 и Т22 - матрицы размера (N-n)xn и (N-n)x(N-n) соответственно, состоящие из коэффициентов левой части уравнений для остальных узлов сетки;
Q - n-мерный вектор-столбец дебитов скважин (значений функции fL,t в точках расположения скважин);
Рк1 и Рк2 - векторы размера n и (N-n), элементы которых получены после переноса в правую часть членов g·Р со значениями Р, соответствующими граничным узлам сетки.
После преобразований, описанных в [4], получим матрицу коэффициентов взаимовлияния скважин по дебиту;
для модели интерференции скважин:
где δР - вектор депрессий скважин.
Коэффициент аij полученной матрицы А показывает, насколько изменится дебит i-й скважины от увеличений депрессии j-й скважины. Очевидно, что увеличение депрессии скважины может вызвать только уменьшение дебитов остальных скважин. Таким образом, коэффициенты взаимовлияния скважин по дебиту - неположительные числа, а коэффициенты самовлияния (диагональные элементы) - положительные.
Отметим, что размерность матрицы А существенно меньше (быть может, на несколько порядков) размерности матрицы исходной системы Т благодаря операции (9). Несмотря на то что такой способ вычисления коэффициентов взаимовлияния предложен весьма давно, на практике по ряду причин (большая размерность системы, плохая обусловленность матрицы системы, неудобство программирования, сложность обращения матриц большой размерности) получить систему уравнений (7), представить ее в виде (8) и проделать операцию (9) для расчета модели взаимовлияния скважин с требуемой точностью вычислений представлялось затруднительным. В итоге решение задач управления группами скважин осложнялось необходимостью поиска альтернативных методов расчета коэффициентов взаимовлияния (например, стохастических методов), что также приводило к неудобству применения таких задач на практике. Автором разработан программный модуль, содержащий алгоритм расчета матрицы коэффициентов взаимовлияния А напрямую, т.е. по формуле (9), в математическом пакете MATLAB, сочетающем в себе преимущества среды программирования и больших возможностей (в том числе и высокой скорости) работы с матрицами. Кроме того, разработанное приложение позволяет сразу же применять полученную модель интерференции скважин при решении задач выбора рациональных способов эксплуатации обустроенного месторождения, то есть задач оптимального управления.
РАЗРАБОТАННЫЙ АЛГОРИТМ ВКЛЮЧАЕТ В СЕБЯ ПОЭТАПНОЕ РЕШЕНИЕ СЛЕДУЮЩИХ ЗАДАЧ:
1) определение шага сетки аппроксимации на основании приведенных в работе соображений;
2) построение аппроксимирующей сетки, выделение граничных и внутренних точек сетки;
3) получение матрицы Т системы уравнений фильтрации;
4) декомпозиция матрицы Т и расчет коэффициентов взаимовлияния.
При решении задач оптимального управления с использованием модели взаимовлияния для задания технологических ограничений удобно перейти от рассмотрения интерференции скважин по дебиту (10) к модели взаимовлияния по депрессии:
Коэффициенты матрицы А - все положительные числа, однако диагональные элементы (коэффициенты самовлияния) значительно больше недиагональных (коэффициентов взаимовлияния по депрессии).
Накладывая технологические ограничения на депрессии скважин для избежания нарушений стабильности гидродинамических процессов в пласте и ограничения на дебиты,

получим следующие уравнения ограничений для решения задач оптимизации:

В качестве примера приведем результаты расчета коэффициентов взаимовлияния скважин на небольшом участке (площадью около 16 кв. м2) одного из месторождений Западной Сибири, на котором расположено 5 добывающих скважин. Исходя из приведенных ранее соображений, шаг сетки выбран 120 м (минимальное расстояние между парой скважин составляет 500 м). Результатом аппроксимации по методу конечных разностей является сетка из 1110 точек, среди которых 136 граничных. Коэффициент проницаемости, характеризующий неоднородность породы, зададим всюду одинаковым (к = 400 мДа), за исключением призабойных зон скважин (в точках сетки, где расположены скважины к = 30 мДа). По результатам расчетов получены коэффициенты взаимовлияния по дебитам:

После наложения технологических ограничений на депрессии получим по формуле (13) систему вида

которую можно включать в ограничения при решении оптимизационных задач, описанных ранее.
Метод определения коэффициентов взаимовлияния, использованный в настоящей работе, позволил создать универсальный алгоритм, т.е. такой, что, задавая геометрические параметры месторождения, расположение скважин, характеристики неоднородности породы, мы получаем модель интерференции скважин (с заранее оговоренной точностью), которую мы в дальнейшем включаем в систему ограничений оптимизационной задачи. Для сравнения можно привести методику идентификации коэффициентов взаимовлияния, предложенную в работе [5]. Несмотря на сравнительную простоту вычислительных процедур в работе, для расчета интерференции скважин необходимо провести значительное исследование, включающее расчет некоторых величин, который необходимо осуществлять различными способами в зависимости от геометрических параметров месторождения и других свойств породы и флюида. Другой пример: в работе [4] приведен метод расчета коэффициентов взаимовлияния и решения оптимизационной задачи методом электрогидродинамических аналогий, который также не является универсальным за счет необходимости построения новой сеточной модели на электроинтеграторе для каждого конкретного объекта. Также такой способ характеризуется сложностью определения погрешности решения в связи с трудностью точной реализации условий физического подобия.
 АСУ ТП добычи нефти" border="0" alt=". Структурная схема комплекса технических средств АСУ ТП добычи нефти" width="350" height="292" />
АСУ ТП добычи нефти" border="0" alt=". Структурная схема комплекса технических средств АСУ ТП добычи нефти" width="350" height="292" />
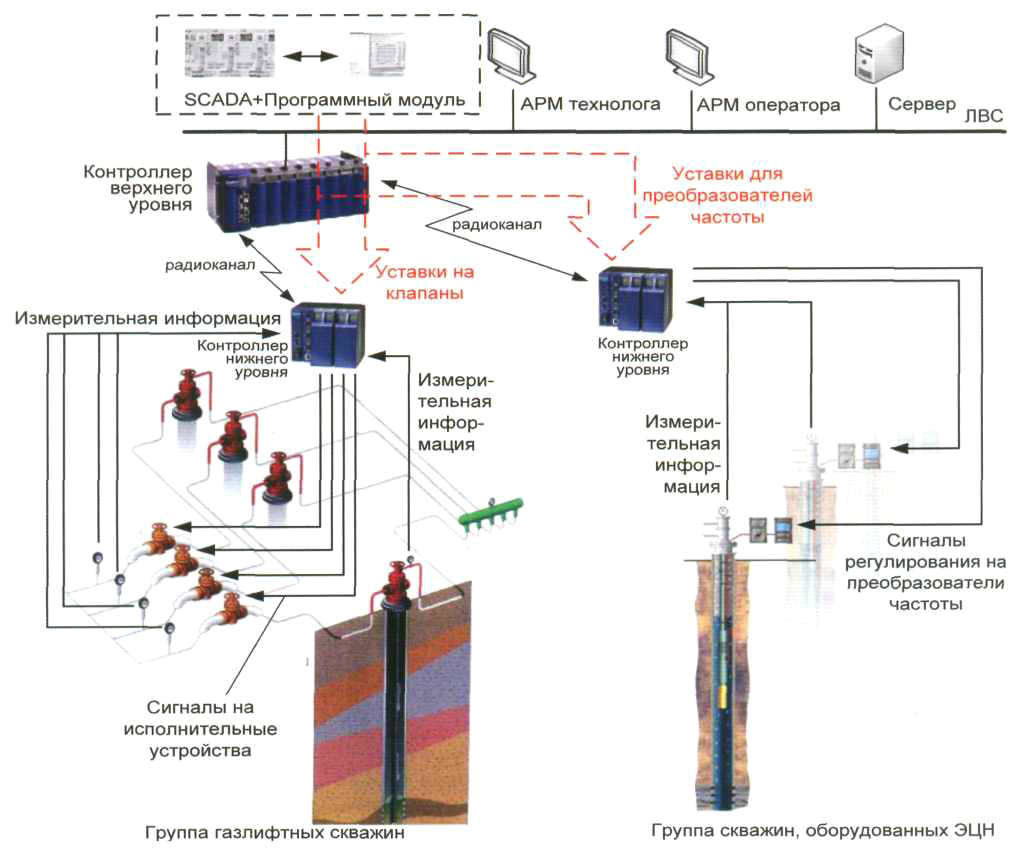
Рис. 3. Структурная схема комплекса технических средств АСУ ТП добычи нефти
ТАКИМ ОБРАЗОМ, АВТОРОМ ПРЕДЛАГАЕТСЯ ВНЕДРИТЬ В АСУ ТП ДОБЫЧИ НЕФТИ РАЗРАБОТАННОЕ ПРИЛОЖЕНИЕ, КОТОРОЕ:
• решает задачи моделирования процесса добычи нефти и оптимального управления режимами эксплуатации скважин в едином программном комплексе;
• взаимодействует со SCADA-системой (по DDE-протоколу), отражающей ход технологического процесса на АРМ технолога;
• вырабатывает уставки для регуляторов, воздействующих на исполнительные механизмы АСУ ТП, как то, регулирующие клапана, установленные в линиях подачи газа в газлифтные скважины, частотные преобразователи, задающие частоту ЭЦН и винтовых насосов, и другие.
Литература:
1. Мастепанов A.M. Топливно-энергетический комплекс России на рубеже веков: состояние, проблемы и перспективы развития. Справочно-аналитический сборник в двух томах. - ИАЦ «Энергия», 2009.
2. Вахитов ГГ. Разностные методы решения задач разработки нефтяных месторождений. - М.: Недра, 1970.
3. ГОСТ Р 8.615-2005 Измерения количества извлекаемой из недр нефти и нефтяного газа. Общие метрологические и технические требования.
4. Мееров М.В., Литвак Б.Л. Оптимизация систем многосвязного управления. - М.: Наука, 1972.
5. Чернов Р.С., Чугунов В.Д. Идентификация значений гидропроводности, приведенных радиусов и коэффициентов взаимовлияния скважин нефтяной залежи по замерам дебитов, забойных и пластовых давлений. Исследования по подземной гидромеханике, 8. - Казань: Издательство Казанского университета, 1986.
6. Мищенко И.Т., Бравичева Т.Б., Ермолаев А.И. Выбор способа эксплуатации скважин нефтяных месторождений с трудноизвлекаемыми запасами. - М.:ФГУП Издательство «Нефти и газ» РТУ нефти и газа им. И.М. Губкина, 2005.
Ю.В. Редуцкий, РГУ нефти и газа имени И.М. Губкина.
Статья опубликована в журнале "Территория нефтебаз" №5, 2011